| La VOCE | COREA | CUBA | JUGOSLAVIA | PALESTINA | RUSSIA | SCIENZA | ARTE |
Stampa pagina |
Stampa inserto |
La VOCE 2006 |
P R E C E D E N T E | S U C C E S S I V A |
| La VOCE | COREA | CUBA | JUGOSLAVIA | PALESTINA | RUSSIA | SCIENZA | ARTE |
Stampa pagina |
Stampa inserto |
La VOCE 2006 |
P R E C E D E N T E | S U C C E S S I V A |
La VOCE ANNO XXII N°10 | giugno 2020 | PAGINA - 42 |
| Copyleft © Tutto il materiale è liberamente riproducibile ed è richiesta soltanto la menzione della fonte. | ||
|
al contrario se le due note risultassero sincrone a maggiori distanze di oscillazioni (la distanza di terza comporta un rapporto di 9:8, quindi diventa sincrona ogni 9 oscillazioni del pendolo più rapido e 8 del più lento) queste sarebbero troppe perché il nostro orecchio ne possa apprezzare la sincronia e quindi risulterebbero dissonanti. a maggior ragione risulterebbero dissonanti con rapporti incommensurabili (ossia con numeri che non hanno un minimo comune multiplo).
come vedremo la sua spiegazione fu semplicistica, ma tornando a pitagora, si pensò di ovviare almeno a questi due inconvenienti studiando una scala con più note (12), ma con intervalli più omogenei: 204cent per le distanze di tono e 96cent per le distanze di semitono: così nacque la scala cromatica pitagorica.
sicuramente la scala cromatica pitagorica risolve il problema della scala pitagorica diatonica di avere a disposizione solo 7 note, però gli altri inconvenienti sono solo attenuati: ad esempio la dissonanza dell'intervallo di terza non viene eliminato del tutto, anche se qui risulta meno stridente (soprattutto però diventa stridente in presenza di strumenti che generano molte armoniche perché ad esempio la quinta armonica naturale di do, 1308hz, risulta molto vicina alla quarta armonica del mi pitagorico, 1332,4hz), inoltre qui la non perfetta consonanza la ritroviamo anche nell'intervallo di sesta.
per di più se si suonasse in una tonalità (per tonalità si intende la scala che prende il nome dalla sua nota di partenza) molto distante da quella indicata a fianco tutti gli strumenti accordati su quella scala risulterebbero sgradevolmente stonati.
per fortuna però la musica greca era prevalentemente melodica, quindi non c'erano sovrapposizioni di voci che non fossero all'unisono o distanziate di un intervallo di quinta, inoltre gli strumenti utilizzati, come ad esempio il flauto, erano molto poveri di armonici superiori.
scala cromatica pitagorica.
nota rapporto frequenza (hz) cent.
do 1:1 261,6 0.
do# 2187:2048 279,4 114.
re 9:8 294,3 204.
mib 32:27 310,1 294.
mi 81:64 331,2 408.
fa 4:3 348,8 498.
fa# 729:512 372,5 612.
sol 3:2 392,4 702.
sol# 6561:4096 419,1 816.
la 27:16 441.5 906.
sib 16:9 465,1 996.
si 243:128 496,7 1110.
do 2:1 523,3 1200.
l'evoluzione musicale.
lo studio delle scale.
però il gigantesco lavoro di pitagora non ha lasciato indifferenti i matematici successivi e già due secoli dopo aristosseno di taranto cominciò a lavorare intorno ad una scala musicale 'temperata equabile', l'argomento fu ulteriormente approfondito da simone stevino nel xvi secolo dell'era volgare e nello stesso periodo dal musicista, padre di galileo, vincenzo galilei.
come si vede la sua adozione fu molto graduale nel tempo e questo per due ragioni, una tecnologica e uno estetico, ossia non esistevano strumenti così precisi per poter fare un'accordatura così precisa e inoltre si andavano a falsare alcuni intervalli pitagorici (ricordate, li abbiamo chiamati intervalli 'giusti'?), che all'orecchio risultavano più 'puri'.
pensate che solo nel 1917 william braid white sviluppò un metodo praticamente utilizzabile per accordare un pianoforte secondo un temperamento equabile rigoroso.
molto prima però si era arrivati ad avere la base di calcolo esatta utilizzando i numeri irrazionali: il rapporto di frequenze che identificava il semitono temperato doveva essere la radice dodicesima di 2 (12√2), un numero irrazionale.
in questo modo dodici semitoni coprono esattamente l'intervallo di un'ottava.
poiché 12√2 ≅ 1,06 ≅ 18/17, il semitono “temperato” risulta essere una via di mezzo tra il semitono cromatico (25/24) e il semitono diatonico (16/15) della scala naturale.
il tono invece vale 12√2x12√2 ≅ 1,1224, quindi è molto più vicino al tono maggiore naturale (9/8=1,125) che al tono minore (10/9 ≅ 1,111).
come conseguenza la terza maggiore temperata è decisamente crescente rispetto alla terza maggiore naturale, che è formata da un tono maggiore e un tono minore.
benché il temperamento equabile sia stato teorizzato prima dell'introduzione in matematica del concetto di logaritmo, l'operazione di suddivisione equabile dell'ottava risulta semplificata se, invece di associare a ciascun intervallo musicale il rapporto fra le frequenze fondamentali delle note che lo compongono, si associa all'intervallo il logaritmo di questo rapporto. infatti in questo modo la giustapposizione di due intervalli consecutivi (ad esempio due toni che formano una terza maggiore). anziché essere rappresentata dal prodotto dei rapporti di frequenze corrispondenti, è rappresentata dalla somma dei rispettivi logaritmi. quindi la suddivisione dell'ottava in semitoni uguali comporta la semplice divisione per 12 del corrispondente valore logaritmico, anziché l'estrazione di una radice dodicesima.
così, gradualmente si arrivò al tetragramma rosso perfezionato da Guido D'Arezzo (902-1050eV), con il quale si scrive ancora oggi la musica gregoriana, ossia il canto monodico (il contrario di polifonico) della liturgia cattolica.
Quel segno che si vede all'inizio del tetragramma rappresenta la chiave di FA e si spostava di rigo in rigo per fare in modo che la melodia stesse sempre dentro il tetragramma. Poi a questo simbolo si aggiunse quello di DO, sempre come richiamo alla precedente notazione delle righe rossa e gialla. 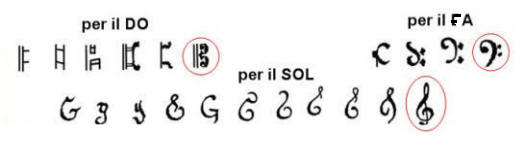 Per fissare l’estensione sonora sul pentagramma della voce umana e degli strumenti musicali, i teorici ricorsero all’uso di tre lettere chiavi e alla definizione delle note in Hertz (baritono e basso=174,6Hz, soprano, mezzosoprano, contralto e tenore=261,6Hz, violino=415.3Hz).
I tre simboli delle chiavi ancor oggi in vigore sono quelle dentro i cerchi rossi.
Per fissare l’estensione sonora sul pentagramma della voce umana e degli strumenti musicali, i teorici ricorsero all’uso di tre lettere chiavi e alla definizione delle note in Hertz (baritono e basso=174,6Hz, soprano, mezzosoprano, contralto e tenore=261,6Hz, violino=415.3Hz).
I tre simboli delle chiavi ancor oggi in vigore sono quelle dentro i cerchi rossi. Solo dopo l'invenzione della stampa (sec. XVI) si arrivò al setticlavio e prese definitivamente forma la grafia sonora tonale, che ha contribuito alla nascita di grandi capolavori della musica europea e all’evoluzione del linguaggio musicale, che si è sempre più raffinato.
Solo dopo l'invenzione della stampa (sec. XVI) si arrivò al setticlavio e prese definitivamente forma la grafia sonora tonale, che ha contribuito alla nascita di grandi capolavori della musica europea e all’evoluzione del linguaggio musicale, che si è sempre più raffinato.Il complesso delle sette chiavi musicali poste all’inizio del pentagramma hanno lo scopo di stabilire una determinata posizione di suoni corrispondente ad ogni voce e strumento. Abbiamo già visto come si debba alla genialità di Guido D'Arezzo anche il nome delle prime sei note, come ancor oggi le conosciamo, ma restava ancora da definire la durata dei suoni. 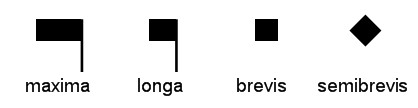 Si inventarono quindi notazioni sempre più complesse.
Si inventarono quindi notazioni sempre più complesse.
Dapprima così e poi così. 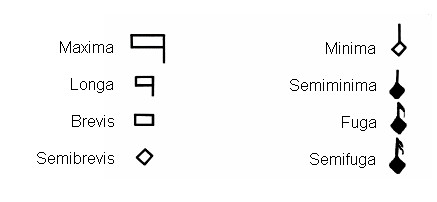 Dalle tre lettere chiavi derivò il setticlavio, il complesso delle sette chiavi musicali che sono segni convenzionali posti all’inizio del pentagramma allo scopo di stabilire una determinata posizione di suoni corrispondente ad ogni voce e strumento.
Dalle tre lettere chiavi derivò il setticlavio, il complesso delle sette chiavi musicali che sono segni convenzionali posti all’inizio del pentagramma allo scopo di stabilire una determinata posizione di suoni corrispondente ad ogni voce e strumento. |
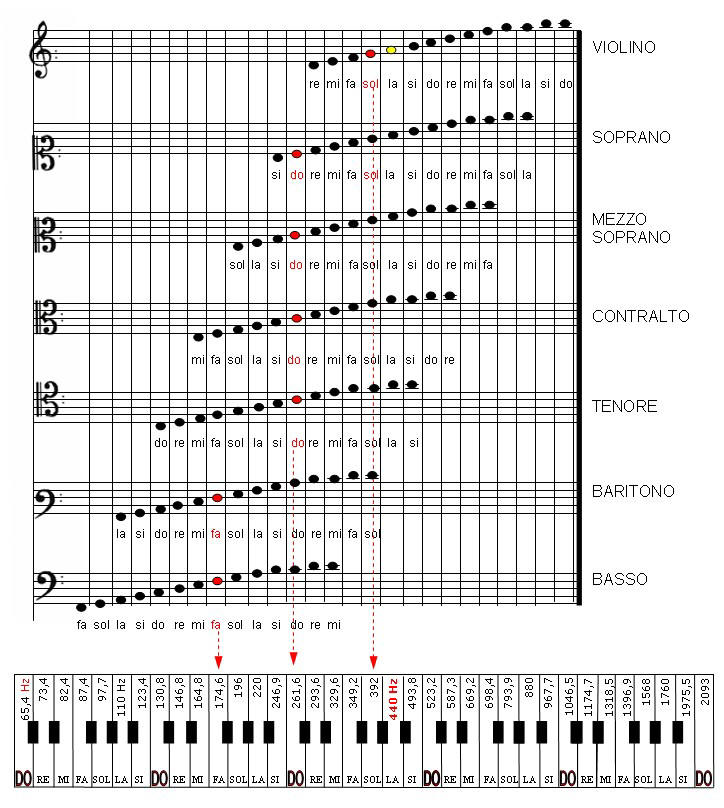 A partire dagli anni '50 si evidenziò una crescente autonomia della timbrica, della durata e in particolar modo dell'altezza sonora intesa come superamento di ogni genere di notazione rigida a favore dell'improvvisazione. Nacquero così le più disparate proposte per ampliare la gamma sonora, timbrica e di durata come richiesta dai nuovi criteri esecutivo e compositivi degli autori contemporanei. Ai nostri giorni, nell'attesa di una chiarificazione e definizione di un sistema di segni realmente organico, riferito alle sonorità e ai suoni musicali, è esplosa l'alta tecnologia musicale che si sta imponendo con un suo linguaggio. Un linguaggio non immediatamente comprensibile, ma pieno di risorse per concretizzare l'evolversi della musica, dove si cela un mondo estremamente complesso e misterioso. 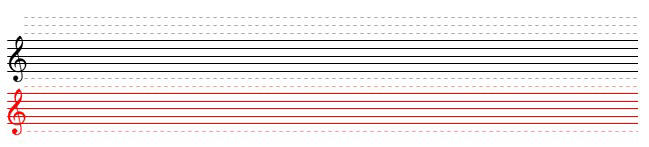 Un contributo per semplificare il codice dell'altezza sonora tonale nella tastiera elettronica è nato il Pentagramma musicale Betba.
Un contributo per semplificare il codice dell'altezza sonora tonale nella tastiera elettronica è nato il Pentagramma musicale Betba.
Il pentagramma Betba è composto da due gruppi di linee colorate per fissare sulla carta l'altezza sonora in Hz in un'unica chiave musicale: chiave di SOL (VIOLINO). Il pentagramma nero, con relativi frammenti di linea, racchiude la gamma sonora che va dal DO di 261,6 Hz al DO di 4186 Hz, mentre il pentagramma rosso, con relativi frammenti di linea, racchiude la gamma sonora inferiore che va dal SI di 246,9 Hz al LA di 27,5 Hz. Questo nuovo procedimento porta l'interprete ad eseguire sulla tastiera esercizi e brani musicali senza ricorrere alla lettura in chiave di FA (basso). |
P R E C E D E N T E | S U C C E S S I V A |
Stampa pagina | Stampa inserto | La VOCE 2006 |
| La VOCE | COREA | CUBA | JUGOSLAVIA | PALESTINA | RUSSIA | SCIENZA | ARTE |